Zeno’s Philosophy Explained – Key Paradoxes on Motion, Space, and Logic

Simple English notes on Zeno’s philosophy and paradoxes. Understand how Zeno challenges motion, plurality, space, and the limits of human logic.

Table of Contents:

Zeno’s Defense of Parmenides

Parmenides claimed that change and motion are illusions, and reality is one unchanging being.
He denied plurality (anekta), saying there are no many things—only one continuous existence.
He also rejected the idea of space or void, believing that nothing can exist outside being itself.
Because of these radical ideas, many mocked Parmenides, thinking his philosophy was unrealistic.
His student Zeno of Elea, about 25 years younger, aimed to defend his teacher’s ideas.
Zeno wrote a book with 40–50 arguments, of which 10 survive today.
His goal was not to prove Parmenides directly, but to show that those who believe in change and motion fall into logical contradictions.
For example, critics said change and motion are real, but Zeno showed that accepting motion creates more problems than denying it.
Thus, his arguments were against the critics, revealing the foolishness of their assumptions.

Summary:
Zeno of Elea defended Parmenides by using logical arguments to challenge those who believed in motion and change. Instead of proving Parmenides right, he exposed contradictions in his opponents’ beliefs, showing that accepting change leads to deeper confusion.

Understanding Zeno’s Paradoxes

Zeno used the same reasoning method as Parmenides, called reductio ad absurdum—proving an opponent wrong by showing their ideas lead to absurd results.
His famous arguments are known as Zeno’s paradoxes.
A paradox is a statement that contradicts itself yet seems true, creating logical confusion.
Example: “I am lying.” If this is true, then it’s false; and if it’s false, then it’s true—forming a logical loop.
A fun example: Ramesh waited all day to be fooled on April Fool’s Day, but nothing happened. In the end, not fooling him became the way he was fooled — a real-life paradox.
Another classic paradox is the Barber Paradox: A barber shaves only those who do not shave themselves. The question — “Does the barber shave himself?” — has no consistent answer.
Paradoxes are not just tricks; they help us think beyond ordinary logic and expand our understanding.
They challenge our assumptions about truth, logic, and reasoning.
The term Philoparadoxia means “one who loves paradoxes” — someone who enjoys exploring such thought-provoking puzzles.

Summary:
Zeno’s paradoxes use the method of reducing an argument to absurdity to expose contradictions in common beliefs. Through examples like the liar and barber paradoxes, we learn how paradoxes challenge normal thinking and encourage deeper philosophical reflection.

The Millet Argument – Against the Senses

Zeno’s first category of paradoxes is called arguments against the senses.
The example he gives is known as the Millet Argument (from millet = bajra).
Zeno says: when a single millet seed falls to the ground, no sound is heard.
But when a full box of millet seeds falls, it makes a loud sound.
There are only two possibilities:
- Either each seed makes a sound, or
- No single seed makes any sound.
If each seed makes a sound but we don’t hear it, then our senses deceive us.
And if each seed makes no sound, then when we do hear the box fall, our senses again deceive us.
Thus, in both cases, Zeno concludes that our senses are unreliable and cannot be trusted for truth.

Summary:
In the Millet Argument, Zeno shows that our senses give conflicting information. Whether we hear or don’t hear sound, our sensory experience leads to contradiction. Therefore, he argues that sense perception is deceptive and cannot reveal true reality.

The Argument Against Plurality

Zeno’s second category of paradoxes is his argument against plurality (anekta or multiplicity).
He begins by assuming that the world contains many objects — like a pen, a mobile, or a laptop.
Zeno says that any single object, like this pen, can be divided infinitely in principle.
For example, a 10-inch pen can be divided into 5 inches, then 2.5 inches, and so on — never reaching zero.
This means that every object is made up of infinite parts or infinite units.
Now, Zeno considers two possibilities:
1. Each part has some size. If so, combining infinite parts will give infinite size — meaning every object would be infinitely large.
2. Each part has no size. If so, adding up infinite parts with zero size will result in no size at all — meaning every object would be infinitely small.
Both conclusions are absurd, since objects are neither infinitely large nor infinitely small.
Therefore, Zeno argues that the belief in plurality (many objects) leads to contradiction.
He supports Parmenides’ view that reality is one indivisible being, without separate parts.

Summary:
Zeno’s argument against plurality shows that if we assume many objects exist, we face two impossible outcomes — everything becomes either infinitely large or infinitely small. Through this reasoning, he supports Parmenides’ idea that true reality is one single, indivisible existence.

Arguments Against Plurality and Space

Zeno adds another argument against plurality (anekta) to show its logical problems.
He says if many objects exist, we must know how many there are — they should have a definite number.
If they have a fixed number, they are finite. But Zeno argues they cannot be finite, because between any two objects, there must be another object separating them.
Similarly, between the first and third object, there is always another — this continues infinitely.
Thus, the objects become infinite in number, yet we also call them finite to count them — a contradiction.
Therefore, it is foolish to believe that multiple objects can exist that are both finite and infinite at the same time.

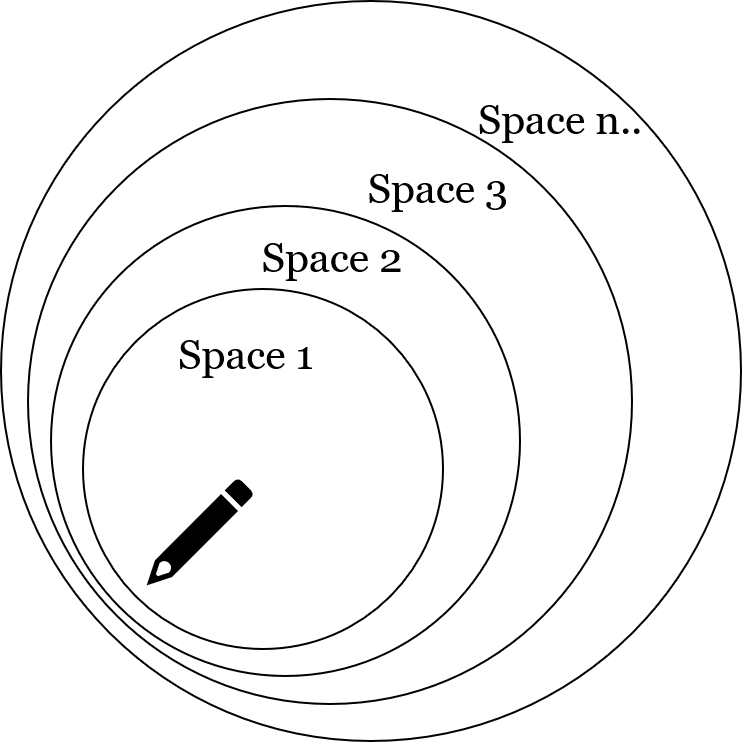
Arguments Against Space

Zeno’s third category of paradoxes targets the idea of space or void.
Parmenides had already said that empty space does not exist.
Zeno argues that if space exists, then it must itself exist in another space.
For example, if a pen exists in space, then that space must also exist somewhere — inside another space.
This leads to an infinite regress of spaces within spaces, which is logically absurd.
Therefore, believing in the existence of space is just as foolish as denying it without reason.

Summary:
Zeno’s second argument against plurality shows that accepting many objects leads to contradiction—they become both finite and infinite. His third argument challenges the concept of space itself, showing that if space exists, it must exist within another, leading to infinite spaces. Both ideas reveal the logical impossibility of plurality and space, supporting Parmenides’ claim that reality is one and indivisible.

Arguments Against Motion

Zeno’s fourth and most famous category of paradoxes is his argument against motion (gati or change).
He claimed that movement is logically impossible, even though it appears real to our senses.

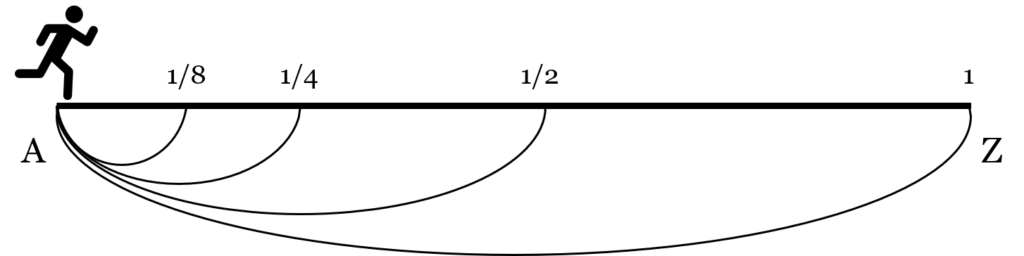
The Racecourse Argument

Imagine a runner who must go from point A to point Z to finish a race.
To reach Z, he must first reach the halfway point between A and Z.
Before reaching that halfway point, he must cover half of that half, and so on.
The distance can be divided infinitely—each time into smaller halves.
Since the runner must cross infinite points, he can never start or finish the race in finite time.
Therefore, motion becomes impossible, because crossing infinite divisions cannot happen in real time.

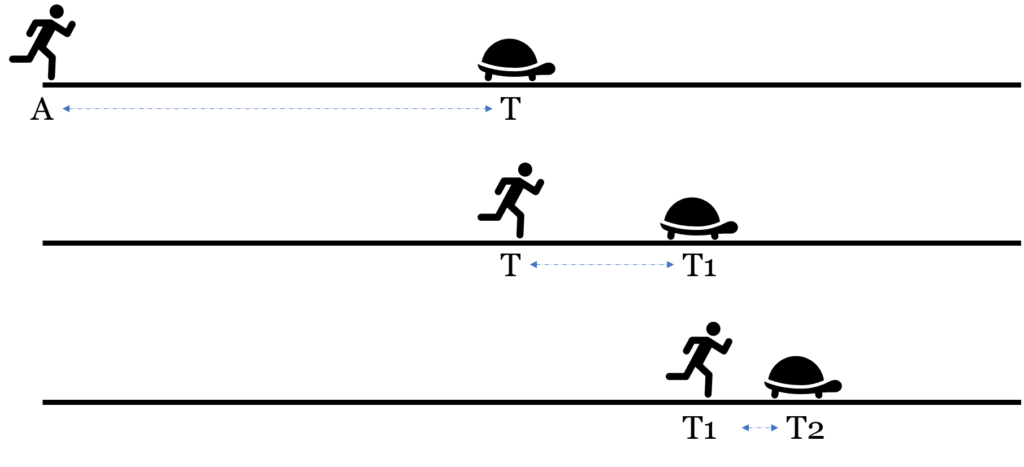
The Achilles and the Tortoise Paradox

In another version, Achilles, a fast runner, races a tortoise and gives it a head start.
To overtake the tortoise, Achilles must first reach the point (T) where the tortoise began.
But by the time Achilles reaches T, the tortoise has moved a little ahead to T₁.
When Achilles reaches T₁, the tortoise moves to T₂, and this continues endlessly.
Thus, Achilles can never actually overtake the tortoise, because there will always be some distance left, no matter how small.
Zeno uses this to argue that motion and change are illusions, not rationally possible events.

Summary:
Zeno’s paradoxes against motion, such as the Racecourse and Achilles and Tortoise, show that movement involves crossing infinitely many divisions, which is logically impossible. Therefore, motion, though seen by the senses, is only an illusion, reinforcing Parmenides’ belief that true reality is motionless and unchanging.

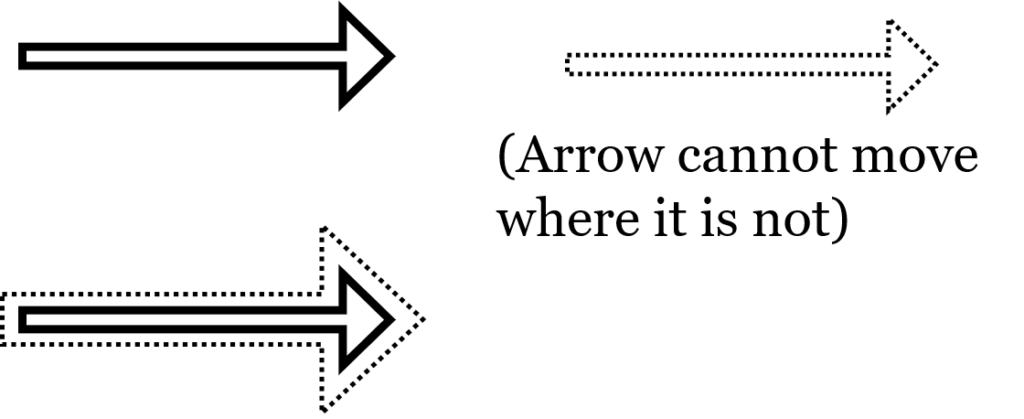
The Moving Arrow Argument

Zeno’s next paradox is called “The Moving Arrow”, which challenges the possibility of motion even more directly.
Common sense tells us that a flying arrow moves through the air, but Zeno questions how and where it actually moves.
He says there are only two possible answers:
1. The arrow moves where it is, or
2. The arrow moves where it is not.
The second option is impossible — the arrow cannot move where it is not, because it simply does not exist there.
The first option is also impossible — if the arrow is where it is, that means it is fully occupying a fixed position in space at that instant.
Something that completely occupies a specific place cannot move while it is in that place.
Therefore, at every moment of time, the arrow is motionless, simply occupying space.
If at every instant the arrow is at rest, then motion is an illusion — the arrow only appears to move when viewed over time.

Summary:
In the Moving Arrow Paradox, Zeno argues that at any given instant, an arrow is stationary because it fully occupies its position in space. Since every moment is like this, the arrow — and by extension, all motion — is impossible. This paradox reinforces Zeno’s claim that change and movement are illusions created by perception.

Reductio ad Absurdum and the Moving Blocks

In this section, Zeno’s reasoning method becomes very clear — it is called reductio ad absurdum (reduction to absurdity).
The method works by assuming the opposite of what you want to prove and then showing that the assumption leads to a contradiction.
Zeno wants to prove: “The arrow cannot move.”
So, he first assumes the opposite: “The arrow can move.”
From this assumption, two possibilities arise — the arrow moves where it is, or where it is not.
As seen earlier, both possibilities are impossible, so the assumption itself fails.
Therefore, the original claim — that the arrow cannot move — must be true.
This logical technique is the core of Zeno’s philosophy, and it later became a fundamental tool in logic and mathematics.

The Moving Blocks Argument

Zeno also gives another lesser-known paradox called the Moving Blocks Argument.
In this setup, there are three blocks — A, B, and C, each 8 feet long.
Block A is stationary, meaning it does not move.
Blocks B and C move in opposite directions with equal speed.
This example is used to explore relative motion and how motion appears contradictory when viewed from different reference points.
Though complex, it continues Zeno’s theme — to show that motion leads to logical absurdities when analyzed carefully.

Summary:
Zeno’s reductio ad absurdum method proves motion impossible by showing contradictions in its opposite claim. His Moving Blocks Argument further examines how relative motion creates logical confusion, strengthening his view that movement and change are illusions, not true aspects of reality.

Legacy and Impact of Zeno’s Paradoxes

At first glance, Zeno’s paradoxes may seem strange or even foolish, but history shows that great discoveries often challenge common sense.
For example, once it was hard to believe that the Earth moves and the Sun stands still, yet that turned out to be true.
Similarly, modern quantum science presents ideas even more shocking than those of Parmenides — even scientists themselves struggle to fully believe them.
Though many mocked Parmenides and Zeno, others recognized the depth and logic behind their thinking.
The great philosopher Aristotle said that Zeno invented a new method of philosophical reasoning — one that accepts an opponent’s view only to show its hidden contradictions.
Zeno’s paradoxes introduced deep questions about motion, change, and infinity, which traditional mathematics could not explain.
These paradoxes directly inspired Newton and Leibniz to develop Calculus, a tool designed to understand infinite division and continuous change.
Later, German mathematician Georg Cantor used similar ideas to create the modern theory of infinite sets, a major advance in mathematical philosophy.
Thus, Zeno’s work, though ancient, laid the foundation for modern mathematics and logic.

Summary:
Zeno’s paradoxes, once mocked as nonsense, became turning points in the history of thought. They challenged assumptions about motion and infinity, leading to the birth of calculus and the theory of infinite sets. His method of reasoning showed that philosophy and science grow by questioning what seems obvious, making Zeno one of the true pioneers of logical thought.

Zeno’s Influence on Logic and Language

Zeno’s paradoxes not only shaped metaphysics and mathematics but also helped in the development of logic.
Classical logic cannot handle contradictions or paradoxes. For example, the statement “The sky is blue and the sky is not blue” is inconsistent — classical logic simply rejects it.
To address such contradictions, philosophers developed paraconsistent logic, a non-classical logic that can meaningfully deal with inconsistent or paradoxical situations.
This shows how Zeno’s paradoxes pushed logical thinking forward, leading to new systems of reasoning.

Role of Language in Zeno and Parmenides’ Philosophy

Both Parmenides and Zeno relied heavily on language to construct their arguments.
Many of their paradoxes arise because words have multiple meanings, and these differences affect logic.
For example, Parmenides said we cannot say “there is nothing,” because the word ‘is’ means existence, while ‘nothing’ means non-existence — and both cannot coexist.
This linguistic confusion deeply influences logical conclusions.
The word ‘is’ itself has different uses in language:
- “There is Socrates” — here, is means existence.
- “Socrates is a philosopher” — here, is shows identity.
- “Socrates is old and wise” — here, is expresses quality or attribute.
These variations show that language shapes logic, and unclear meanings create confusion in reasoning.
Understanding such differences is essential in the philosophy of language, which studies how words influence truth and logic.

Summary:
Zeno’s ideas inspired new forms of logic, like paraconsistent logic, to handle contradictions that classical logic could not. His and Parmenides’ use of language showed how meaning affects reasoning—a single word like “is” can change the logic of an entire statement. Their work laid the foundation for exploring how language, logic, and reality are deeply interconnected.

philoparadoxia